Ejercicio 6: Programación lineal "Método gráfico"

Ecuación general:

P=25x + 12y

Sujeto a:

30x + 9y <= 150

8x + 20y <= 120

x,y >=0

Ec1: 30x + 9y= 150

Cuando: x=0, y=150/9

y=16.67

Cuando: y=0, x=150/30

x=5

Ec2: 8x + 20y=120

Cuando: x=0, y=30/5

y=6

Cuando: y=0, x=30/2

x=15

Gráfica:

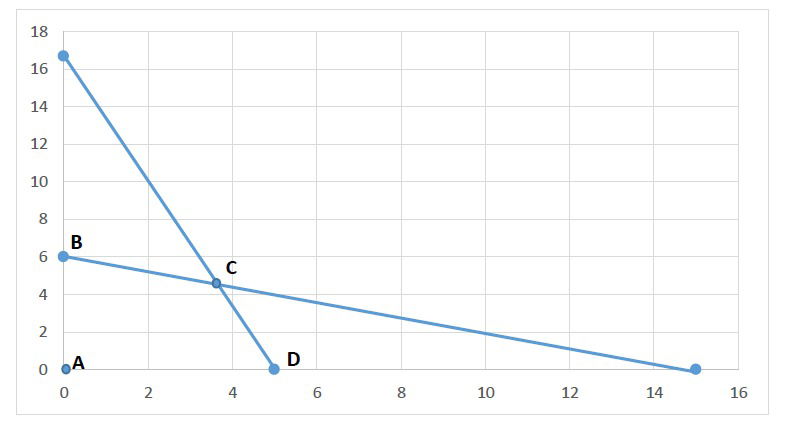
Coordenas de los puntos en la gráfica:

A(0,0)

B(0,6)

D(5,0)

Para encontrar las coordenadas del punto C es necesario hacer lo siguiente:

ec 1. (30x + 9y= 150)(-8)=-240x - 72y = - 1200

ec 2. (8x + 20y=120)(30)= 240x + 600y= 3600

Ahora restamos los resultados de las ecuaciones 1 y 2 y obtenemos el siguiente resultado

528y=2400

Encontrando el valor de y

y=2400/528

y=4.54

Ahora buscamos el valor de x utilizando cualquier ecuacion de la 1 o 2 y sustituyendo el valor de "y"

30x + 9y= 150

30x + 9(4.54)=150

30x + 40.86=150

30x=109.14

x=109.14/30

x=3.64

Coordenadas del punto C

C(3.65, 4.54)

Sustituyendo los datos de las coordenadas en la ecuación: P= 25x + 12y

A(0,0)= 25(0) + 12(0)= $0

B(0,6)= 25(0) + 12(6)= $ 72

C(3.65, 4.54)= 25(3.65) + 12(4.54)= $145.73

D(5,0)= 25(5) + 12(0)= $125

El punto que genera mayor ganancia es el de la coordenada C