Ejercicio 2: Programación Lineal "Método Gráfico"

Las industrias aeronáuticas "COSMOS" tienen 2 plantas: I y II que producen los motores safiro utilizando en guiones ligeros. Las capacidades máximas de producción de cada planta son 100 y 110 unidades/mes. Los motores se envían a dos plantas ensambladoras: A y B, los costos de envió (Dólares) por motor de I y II hacia A y B son:

Para el próximo mes de marzo la planta "A" requiere 80 motores y la planta "B" necesita 70 motores. ¿Cuántos motores deben enviarse de I y II a A y B para que los costos sean MÍNIMOS?

SOLUCIÓN:

Sea "x" el número de motores de la planta I hacia la planta "A".

Sea "y" el número de motores de la planta I hacia la planta "B".

C= 100x + 60y + 120(80-x) + 70(70-y)

C= 100x + 60y + 9600 - 120x + 4900 - 70y

C= -20x - 10y + 14,500

Restricciones

x + y <= 100

(80-x) + (70-y)<= 110

80 - x + 70 - y <=110

150 - x - y<=110

-x - y + 150 - 150 <= 110 - 150

- x - y <= -40

(- x - y <= -40)(-1)

x + y >= 40

 x>=0; y>=0

80-x>=0

(-1)(-x>=80)

x<=80

70 - y>=0

(-1)(-y>=-70)

y<=70

x+y=100

Cuando: y=0, x=100

Cuando: x=0, y=100

x+ y =40

Cuando: y=0, x =40

Cuando: x=0, y =40

x>=80

x=80

y<=70

y=70

Gráfica de los resultados de "x" y "y"

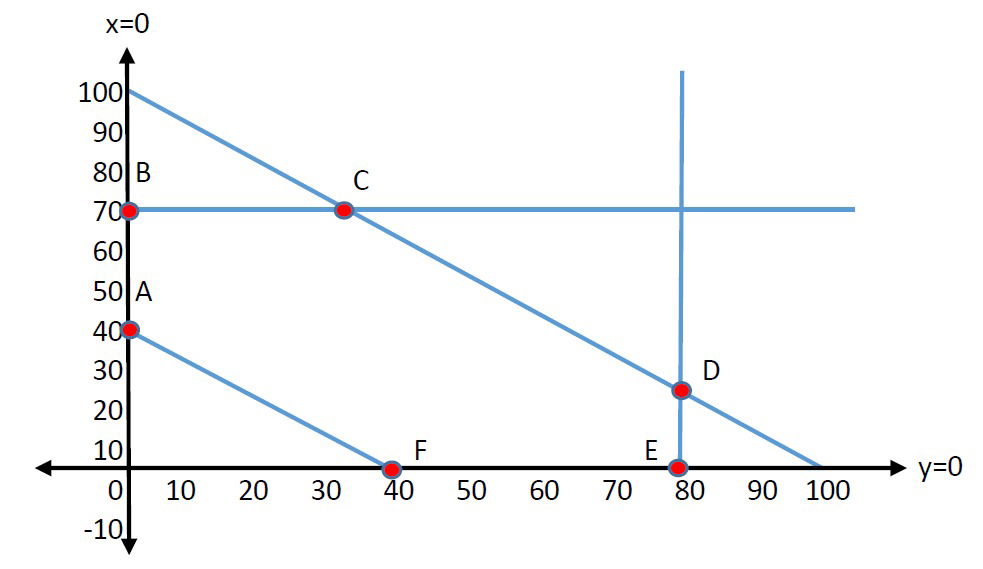
Ahora sacamos las coordenadas de los puntos marcados y sustituimos en la ecuación que anteriormente encontramos:

C= 14,500 - 20x -10y

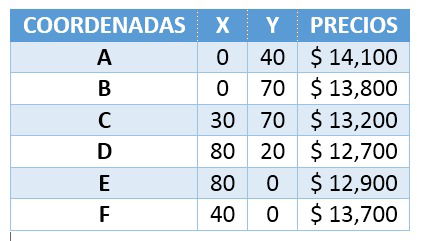
Por lo tanto podemos concluir que el costo mínimo es de $12,700